Sudoku and Solver
Sudoku and Solver
Advanced
@ Although you can solve many samples by mastering the intermediate class, there are also high-level samples that cannot be solved without using special techniques. While the techniques up to the intermediate class are applicable to all Sudoku samples, the advanced class techniques are special ones applicable only if the applicable conditions are met. The fundamental difference from the intermediate class in the technique is that in the advanced class, the conditions and constraints of other areas are used to determine the number of the area. It may take from 40 minutes to 2 hours to solve the sample of the advanced class (sometimes, it may not be possible to solve by logical approach).
1. A Technique 1 (3 cells decision / 3 areas) (Note) Also called XY Wing.
The technique of 3 cells decision / 3 areas is a technique to determine the cell in symmetrical position guiding by 3 cells in 3 symmetrical areas. A technique 1 (3 cells decision / 3 areas) is applied
1. symmetrical 3 areas
2. 3 numbers of different 2 digits
3. appearing 2 times each
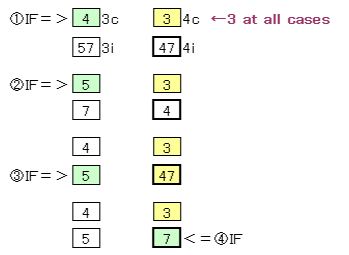
So the combination of 45-57-47 is OK, but 45-45-47 and 45-457-457 can not be applied.
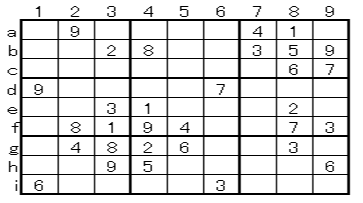
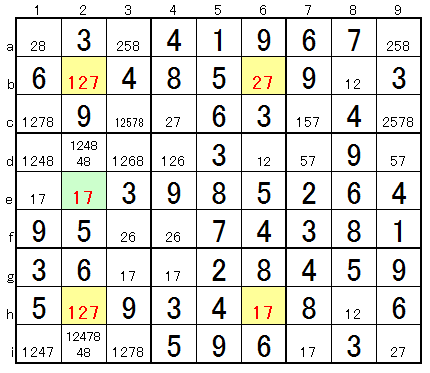
*Advanced Example 1
 @@@@@
@@@@@* Answer procedure
The following results are obtained by the analysis techniques of the beginner and intermediate classes.
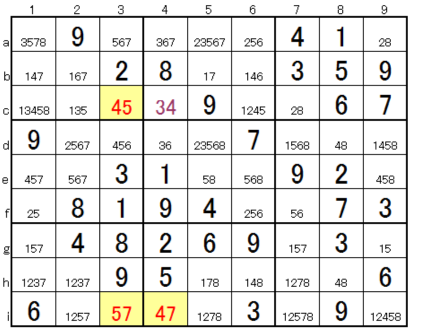
@ Focusing on the 3 yellow cells, they are 45-57-47. As this is learned in the same area, the same column, the same row as the intermediate class, it occupies three numbers. However, if it appears in different cells, it can be applied as the following proof. As a result, B (4c) is determined to be 3. If this is understood, it can be easily solved with the knowledge of the intermediate class.
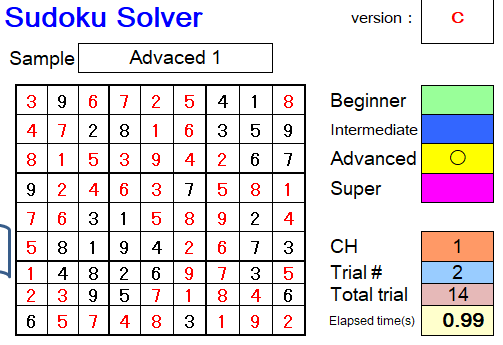
This example takes about 0.99 seconds at advanced level in Sudoku Solver.
2. A Technique 2 (4 cells decision / 2 areas) @
The 4 cells decision / 2 areas technique is a technique that is derived from the 4 cells of the symmetrical 2 areas to determine the empty cell in other areas, and is a relatively frequently applied technique.
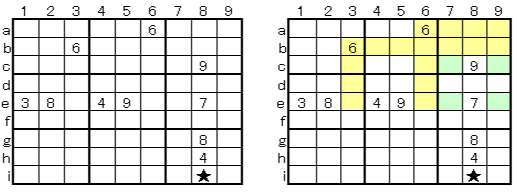
*Advanced Example 2
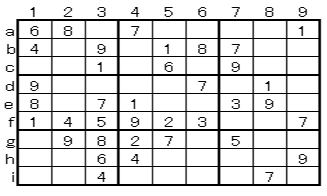
* Answer procedure
It is in the state where the number of the intermediate class is filled in. Green is a possible cell of 1.
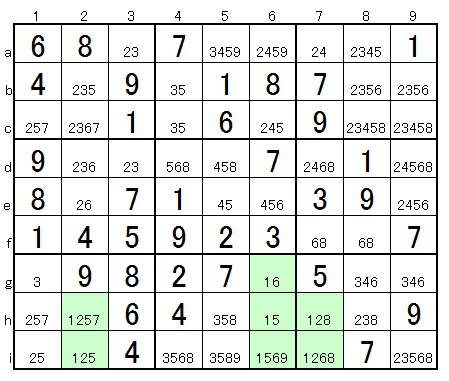
There are 2 cells in rows 2 in the left area G, 3 cells in rows 6 in the middle area H, and 2 cells in rows 7 in the right area I. The left and right areas contain only 2 column hi, so if 1 enters left G (2h), 1 enters right I (7i). Also, if 1 enters left G (2i), 1 enters right I (7h). Therefore, there is only H (6g) that 1 in the area H in the middle can contain. The technique that can be decided from 4 cells in the other 2 areas like this is called the A technique 2 (4 cells decision / 2areas).

Knowing this, you can easily answer the rest.
This example takes 0.96 seconds at advanced level in Sudoku Solver.
@
3. A Technique 3 (4 cells decision / 4 areas) (Note) Also called X wing.
The technique of 4 cells decision / 4 areas is a technique that derives from 4 cells of 4 symmetrical areas and determines empty cell of other area.
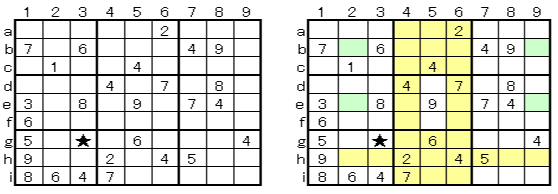
*Advanced Example 3
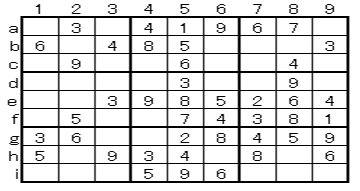 @@@
@@@
* Answer procedure
Look at 7 in column b, h. There are row 2, 6 in which each 7 enters. As shown below, if 7 enters A (b2), 7 enters H(h6). Similarly, if 7 enters G (h2), then B (b6) becomes 7. That is, 7 in the row 2 is limited to A (b2) and G (h2), so 7 does not enter D (e2). Therefore, D (e2) becomes 1. Knowing this, you can easily answer the rest. As it is determined by 4 cells in 4 areas in this way, this is called A technique 3 (4 cells decision / 4 areas).

This example takes about 0.98 seconds at advanced level in Sudoku Solver.
4. A Technique 4 (restricted cell method)
@ The restricted cell method is a technique that determines the number by limiting the number of cells in a certain area. Check each example.
*Advanced Example 4-1
In this example we focus on 6 and . The only 6 possibilities are four green cells C (7c), C (9c), F (7e) and F (9e). There are 6 in row 7,9 of C and F. Therefore, 6 is determined for .
 @@Λ6
@@Λ6*Advanced Example 4-2
Focus on and 2 in the G area. The cells without 2 are shown in yellow. As 2 enters 2 cells in the column b shown in green and 2 enters 2 cells in the column e, 2 does not fit in row 2 of the G area. Therefore, is decided to 2.
 Λ2
Λ2*Advanced Example 4-3
Focus on and 5 in the I area. The cells that do not contain 5 are shown in yellow, but focus on the possible green column b, e, and h that contain 5. As you can see in the example below, 5 is in row 5 , row 7 , or row 9. There is only in area I for 5. will be 5.
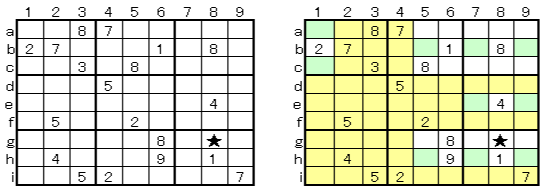 @Λ5
@Λ5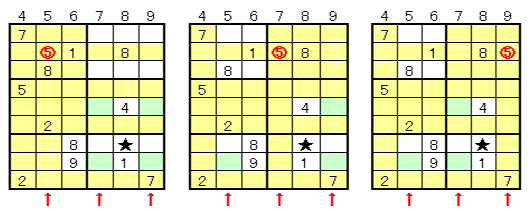
*Advanced Example 4-4
Focus on areas H and 8. It is 3 cells that there is a possibility of entering 8 by H. It becomes an assumption method, but if you try to put 8 in each box, will go in 8 in all cases.
5. A Technique 5 (Assumption method)
(note) It is also called trial and error method, temporary placement method
If the sample can not be solved by using all the techniques known to beginner, intermediate and advanced, use the hypothesis method which is the treasurer of the House. The analysis process proceeds by "provisioning" the possible numbers. If temporary assumption is correct, it will end normally, but if temporary assumption is wrong, a contradiction will occur on the way, so it is possible to know that the number of temporary assumption is incorrect. If it does not end in one temporary placement, you need to make a second temporary placement. If you use the hypothesis method, it takes time, but you can always solve the Sudoku. If the analysis of rationalization using techniques is "brain labor", the assumption method is "physical labor". In the spirit of Sudoku, the Assumption method is the last resort, because of the regular use of the treasurer of House, it is no longer a treasure of House.
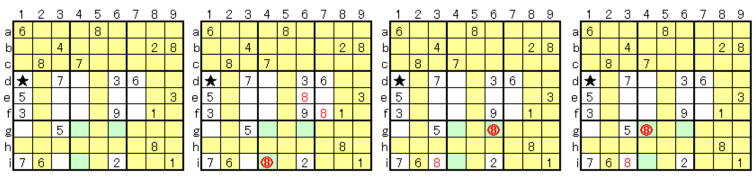
*Advanced Example 5
* Answer procedure
We can not go any further with all the techniques.
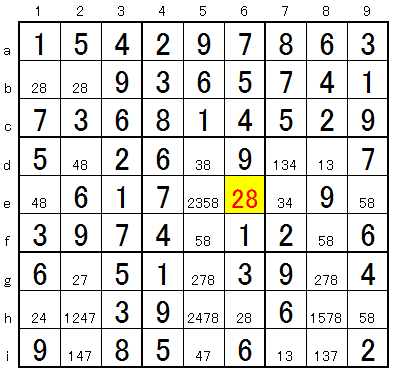
Of the 28 in yellow cell E (6e) in the hypothesis method, it is assumed to be 8 temporarily. On the way, 2 occurred in 2 in row 8, causing a contradiction. We found that we had made a mistake in 8 temporary placements, so we put 2 in. If 2 is temporarily placed, it will end normally.
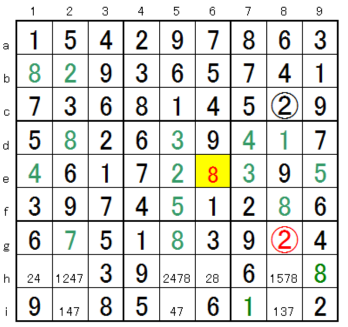
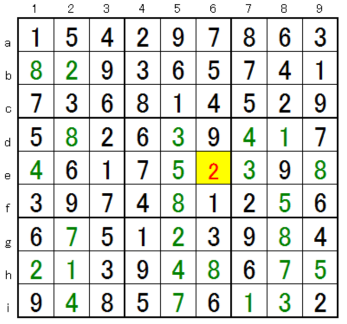
If you understand this, now you can solve 99% of Sudoku samples !